SEPTIMO
Representaciones Gráficas
Tras la recogida de datos, su ordenación y cuantificación, es útil la representación gráfica, ésta nos permite con un simple vistazo obtener información relevante de la población o la muestra.
Hay distintos tipos de representación de datos, dependiendo de qué tipo de carácter estemos estudiando (cualitativo, cuantitativo discreto o continuo) e incluso dentro de un tipo hay representaciones que resumen mejor un determinado concepto que otro.
En el siguiente cuadro resumiremos los distintos tipos de representación gráfica y a qué tipo de carácter se aplica.
|
Gráfica
|
Tipo de datos
|
| Diagrama de sectores | Caracteres cualitativos y cuantitativos |
| Diagrama de barras | Caracteres cualitativos y cuantitavos discretos |
| Diagrama de barras acumulado | Caracteres cuantitativos discretos |
| Histograma | Caracteres cuantitativos continuos |
| Poligonal de frecuencias | Caracteres cuantitativos discretos y continuos |
| Pictograma | Caracteres cualitativos y cuantitativos |
| Cartograma | Caracteres cualitativos y cuantitativos |
Diagrama de barras.
Para realizar esta representación tomamos el primer cuadrante de un sistema de coordenadas donde el eje de abscisas se corresponderá con las modalidades y el de ordenada con las frecuencias, éstas pueden ser absolutas o relativas.
Veamos con un ejemplo como queda.
En una empresa se desea conocer el color de ojos de sus empleados, se observa a los 50 empleados y se obtienen los siguientes resultados:
|
El diagrama de barras asociado es:
 |
En otras ocasiones tenemos los datos de dos variables y queremos representarlos en un mismo diagrama de barras para compararlos, lo más probable es que no haya el mismo número de observaciones en cada una de ellas, por lo que no sería acertado representar el diagrama de barras con las frecuencias absolutas, en este caso las frecuencias relativas son más adecuadas para su representación.
Dos empresas estudian el estado civil de sus empleados con el siguiente resultado:

Diagrama de barras para variables cuantitativas discretas
El procedimiento a seguir es similar al del caso cualitativo, con la salvedad de que ahora podremos obtener también diagramas de barras acumulados, cosa que no era posible determinar en el caso cualitativo.
Consideremos el número de habitantes por vivienda en Andalucia en 2001,según el Instituto Andaluz de Estadística.
La variable número de habitantes es cuantitativa por tanto podemos ordenar sus modalidades y realizar un estudio acumulado.
|
 |
||||||||||||||||||||||
|
 |
Diagrama de sectores.
Se toma un círculo y se divide en tantos sectores como clases tengamos, siendo el arco del círculo proporcional a las frecuencias absolutas (también lo podemos hacer con las frecuencias relativas o porcentajes)
Para determinar el arco circular que corresponde a cada clase relacionamos el total de observaciones con los 360º grados de la circunferencia. Los grados de cada clase vendrán dados por ![]() .
.
Ejemplo
Los resultados en la primera evaluación de un curso de Bachillerato son los siguientes:
| aprobados | 1 suspenso | 2 suspensos | 3 suspensos | 4 o más |
| 7 | 9 | 8 | 5 | 3 |

Fuentes de contaminación acústica en Andalucía
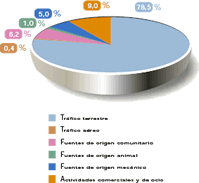
Fuente: Consejería de Medio Ambiente
Polígono de frecuencias
Se obtiene uniendo con segmento los puntos de coordenadas (xi,ni) en el caso en que tomemos las frecuencias absolutas, si fuesen las relativas cambiaríamos ni por f i.
El número de habitantes por vivienda en Andalucia en 2001,según el Instituto Andaluz de Estadística, es el que se adjunta en la tabla, vamos a representar un poligono de frecuencias.
|
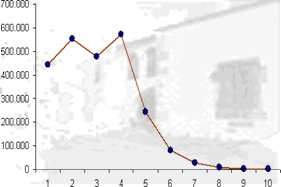 |
||||||||||||||||||||||
| Por otro lado, al tratarse de un caracter cuantitativo podemos ordenar los datos y realizar una representación de los datos acumulados, en este caso tomamos Ni en lugar de ni Poligonal acumulada. |
|||||||||||||||||||||||
|
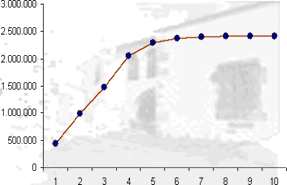 |
||||||||||||||||||||||
Pictograma
Son gráficos con dibujos alusivos al carácter que se está estudiando y cuyo tamaño es proporcional a las frecuencias que representan.
Tomemos el Padrón Municipal de Habitantes a 1 de Enero de 2005, podemos hacer una representación gráfica de los habitantes de cada una de las 8 provincias de Andalucía. Una imagen alusiva será la figura de una persona, cuyo tamaño estará relacionado con el número de habitantes de cada provincia.
El pictograma correspondiente es el que sigue:

Histograma
Una variable continua puede tomar todos los valores comprendidos en un rango. Para clasificar los datos se cogen intervalos, a ser posible, de amplitud constante. Una vez ordenados los datos en una tabla podremos construir una gráfica que represente esos datos.
La representación son rectángulos cuya área es proporcional a la frecuencia de cada modalidad, en el caso de que los intervalos que se tomen sean iguales, las alturas de los rectángulos se pueden tomar iguales a las frecuencias correspondientes.
- Histograma con intervalos constantes
La esperanza de vida de un hombre al nacer viene dada por la tabla que se adjunta, como se observa los intervalos en que se divide son de amplitud constante, entonces se puede representar el histograma correspondiente tomandoPeriodoEsperanza de vida[1951,1956) 58,60 [1956,1960) 63,75 [1961,1966) 66,51 [1966,1971) 67,67 [1971,1976) 68,42 [1976,1981) 69,69 [1981,1986) 71,97 [1986,1991) 72,58 [1991,1996) 73,19 [1996,2000] 74,20 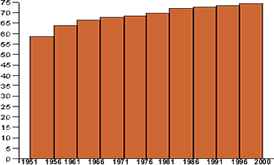
Definición de parámetro estadístico
Un parámetro estadístico es un número que se obtiene a partir de los datos de una distribución estadística.
Los parámetros estadísticos sirven para sintetizar la información dada por una tabla o por una gráfica.
Tipos de parámetros estadísticos
Hay tres tipos parámetros estadísticos:
De centralización.
De posición
De dispersión.
Medidas de centralización
Nos indican en torno a qué valor (centro) se distribuyen los datos.
La medidas de centralización son:
Media aritmética
La media es el valor promedio de la distribución.
Mediana
La mediana es la puntación de la escala que separa la mitad superior de la distribución y la inferior, es decir divide la serie de datos en dos partes iguales.
Moda
La moda es el valor que más se repite en una distribución.
Definición de moda
La moda es el valor que tiene mayor frecuencia absoluta.
Se representa por Mo.
Se puede hallar la moda para variables cualitativas y cuantitativas.
Hallar la moda de la distribución:
2, 3, 3, 4, 4, 4, 5, 5 Mo= 4
Si en un grupo hay dos o varias puntuaciones con la misma frecuencia y esa frecuencia es la máxima, la distribución es bimodal o multimodal, es decir, tiene varias modas.
1, 1, 1, 4, 4, 5, 5, 5, 7, 8, 9, 9, 9Mo= 1, 5, 9
Cuando todas las puntuaciones de un grupo tienen la misma frecuencia, no hay moda.
2, 2, 3, 3, 6, 6, 9, 9
Si dos puntuaciones adyacentes tienen la frecuencia máxima, la moda es el promedio de las dos puntuaciones adyacentes.
0, 1, 3, 3, 5, 5, 7, 8Mo = 4
Cálculo de la moda para datos agrupados
1º Todos los intervalos tienen la misma amplitud.
![]()
Li es el límite inferior de la clase modal.
fi es la frecuencia absoluta de la clase modal.
fi--1 es la frecuencia absoluta inmediatamente inferior a la clase modal.
fi-+1 es la frecuencia absoluta inmediatamente posterior a la clase modal.
ai es la amplitud de la clase.
También se utiliza otra fórmula de la moda que da un valor aproximado de ésta:
![]()
Ejemplo
Calcular la moda de una distribución estadística que viene dada por la siguiente tabla:
| fi | |
|---|---|
| [60, 63) | 5 |
| [63, 66) | 18 |
| [66, 69) | 42 |
| [69, 72) | 27 |
| [72, 75) | 8 |
| 100 |

![]()
2º Los intervalos tienen amplitudes distintas.
En primer lugar tenemos que hallar las alturas.
![]()
La clase modal es la que tiene mayor altura.
![]()
La fórmula de la moda aproximada cuando existen distintas amplitudes es:
![]()
Ejemplo
En la siguiente tabla se muestra las calificaciones (suspenso, aprobado, notable y sobresaliente) obtenidas por un grupo de 50 alumnos. Calcular la moda.
| fi | hi | |
|---|---|---|
| [0, 5) | 15 | 3 |
| [5, 7) | 20 | 10 |
| [7, 9) | 12 | 6 |
| [9, 10) | 3 | 3 |
| 50 |
![]()
![]()
Definición de mediana
Es el valor que ocupa el lugar central de todos los datos cuando éstos están ordenados de menor a mayor.
La mediana se representa por Me.
La mediana se puede hallar sólo para variables cuantitativas.
Cálculo de la mediana
1 Ordenamos los datos de menor a mayor.
2 Si la serie tiene un número impar de medidas la mediana es la puntuación central de la misma.
2, 3, 4, 4, 5, 5, 5, 6, 6Me= 5
3 Si la serie tiene un número par de puntuaciones la mediana es la media entre las dos puntuaciones centrales.
7, 8, 9, 10, 11, 12Me= 9.5
Cálculo de la mediana para datos agrupados
La mediana se encuentra en el intervalo donde la frecuencia acumulada llega hasta la mitad de la suma de las frecuencias absolutas.
Es decir tenemos que buscar el intervalo en el que se encuentre ![]() .
.

Li es el límite inferior de la clase donde se encuentra la mediana.
![]() es la semisuma de las frecuencias absolutas.
es la semisuma de las frecuencias absolutas.
Fi-1 es la frecuencia acumulada anterior a la clase mediana.
ai es la amplitud de la clase.
La mediana es independiente de las amplitudes de los intervalos.
Ejemplo
Calcular la mediana de una distribución estadística que viene dada por la siguiente tabla:
| fi | Fi | |
|---|---|---|
| [60, 63) | 5 | 5 |
| [63, 66) | 18 | 23 |
| [66, 69) | 42 | 65 |
| [69, 72) | 27 | 92 |
| [72, 75) | 8 | 100 |
| 100 |
100/2 = 50
Clase de la mediana: [66, 69)
![]()
Definición de mediana
Es el valor que ocupa el lugar central de todos los datos cuando éstos están ordenados de menor a mayor.
La mediana se representa por Me.
La mediana se puede hallar sólo para variables cuantitativas.
Cálculo de la mediana
1 Ordenamos los datos de menor a mayor.
2 Si la serie tiene un número impar de medidas la mediana es la puntuación central de la misma.
2, 3, 4, 4, 5, 5, 5, 6, 6Me= 5
3 Si la serie tiene un número par de puntuaciones la mediana es la media entre las dos puntuaciones centrales.
7, 8, 9, 10, 11, 12Me= 9.5
Cálculo de la mediana para datos agrupados
La mediana se encuentra en el intervalo donde la frecuencia acumulada llega hasta la mitad de la suma de las frecuencias absolutas.
Es decir tenemos que buscar el intervalo en el que se encuentre ![]() .
.

Li es el límite inferior de la clase donde se encuentra la mediana.
![]() es la semisuma de las frecuencias absolutas.
es la semisuma de las frecuencias absolutas.
Fi-1 es la frecuencia acumulada anterior a la clase mediana.
ai es la amplitud de la clase.
La mediana es independiente de las amplitudes de los intervalos.
Ejemplo
Calcular la mediana de una distribución estadística que viene dada por la siguiente tabla:
| fi | Fi | |
|---|---|---|
| [60, 63) | 5 | 5 |
| [63, 66) | 18 | 23 |
| [66, 69) | 42 | 65 |
| [69, 72) | 27 | 92 |
| [72, 75) | 8 | 100 |
| 100 |
100/2 = 50
Clase de la mediana: [66, 69)
![]()
Definición de media aritmética
La media aritmética es el valor obtenido al sumar todos los datos y dividir el resultado entre el número total de datos.
![]() es el símbolo de la media aritmética.
es el símbolo de la media aritmética.
![]()

Ejemplo
Los pesos de seis amigos son: 84, 91, 72, 68, 87 y 78 kg. Hallar el peso medio.
![]()
Media aritmética para datos agrupados
Si los datos vienen agrupados en una tabla de frecuencias, la expresión de la media es:
![]()

Ejercicio de media aritmética
En un test realizado a un grupo de 42 personas se han obtenido las puntuaciones que muestra la tabla. Calcula la puntuación media.
| xi | fi | xi · fi | |
|---|---|---|---|
| [10, 20) | 15 | 1 | 15 |
| [20, 30) | 25 | 8 | 200 |
| [30,40) | 35 | 10 | 350 |
| [40, 50) | 45 | 9 | 405 |
| [50, 60 | 55 | 8 | 440 |
| [60,70) | 65 | 4 | 260 |
| [70, 80) | 75 | 2 | 150 |
| 42 | 1 820 |
![]()
Propiedades de la media aritmética
1. La suma de las desviaciones de todas las puntuaciones de una distribución respecto a la media de la misma igual a cero.
![]()
La suma de las desviaciones de los números 8, 3, 5, 12, 10 de su media aritmética 7.6 es igual a 0:
8 − 7.6 + 3 − 7.6 + 5 − 7.6 + 12 − 7.6 + 10 − 7.6 =
= 0. 4 − 4.6 − 2.6 + 4. 4 + 2. 4 = 0
2. La suma de los cuadrados de las desviaciones de los valores de la variable con respecto a un número cualquiera se hace mínima cuando dicho número coincide con la media aritmética.
![]()
3. Si a todos los valores de la variable se les suma un mismo número, la media aritmética queda aumentada en dicho número.
4. Si todos los valores de la variable se multiplican por un mismo número la media aritmética queda multiplicada por dicho número.
Observaciones sobre la media aritmética
1. La media se puede hallar sólo para variables cuantitativas.
2. La media es independiente de las amplitudes de los intervalos.
3. La media es muy sensible a las puntuaciones extremas. Si tenemos una distribución con los siguientes pesos:
65 kg, 69kg , 65 kg, 72 kg, 66 kg, 75 kg, 70 kg, 110 kg.
La media es igual a 74 kg, que es una medida de centralización poco representativa de la distribución.
4. La media no se puede calcular si hay un intervalo con una amplitud indeterminada.
| xi | fi | |
|---|---|---|
| [60, 63) | 61.5 | 5 |
| [63, 66) | 64.5 | 18 |
| [66, 69) | 67.5 | 42 |
| [69, 72) | 70.5 | 27 |
| [72, ∞ ) | 8 | |
| 100 |
En este caso no es posible hallar la media porque no podemos calcular la marca de clase de último intervalo.
Definición de media aritmética
La media aritmética es el valor obtenido al sumar todos los datos y dividir el resultado entre el número total de datos.
![]() es el símbolo de la media aritmética.
es el símbolo de la media aritmética.
![]()

Ejemplo
Los pesos de seis amigos son: 84, 91, 72, 68, 87 y 78 kg. Hallar el peso medio.
![]()
Media aritmética para datos agrupados
Si los datos vienen agrupados en una tabla de frecuencias, la expresión de la media es:
![]()

Ejercicio de media aritmética
En un test realizado a un grupo de 42 personas se han obtenido las puntuaciones que muestra la tabla. Calcula la puntuación media.
| xi | fi | xi · fi | |
|---|---|---|---|
| [10, 20) | 15 | 1 | 15 |
| [20, 30) | 25 | 8 | 200 |
| [30,40) | 35 | 10 | 350 |
| [40, 50) | 45 | 9 | 405 |
| [50, 60 | 55 | 8 | 440 |
| [60,70) | 65 | 4 | 260 |
| [70, 80) | 75 | 2 | 150 |
| 42 | 1 820 |
![]()
Propiedades de la media aritmética
1. La suma de las desviaciones de todas las puntuaciones de una distribución respecto a la media de la misma igual a cero.
![]()
La suma de las desviaciones de los números 8, 3, 5, 12, 10 de su media aritmética 7.6 es igual a 0:
8 − 7.6 + 3 − 7.6 + 5 − 7.6 + 12 − 7.6 + 10 − 7.6 =
= 0. 4 − 4.6 − 2.6 + 4. 4 + 2. 4 = 0
2. La suma de los cuadrados de las desviaciones de los valores de la variable con respecto a un número cualquiera se hace mínima cuando dicho número coincide con la media aritmética.
![]()
3. Si a todos los valores de la variable se les suma un mismo número, la media aritmética queda aumentada en dicho número.
4. Si todos los valores de la variable se multiplican por un mismo número la media aritmética queda multiplicada por dicho número.
Observaciones sobre la media aritmética
1. La media se puede hallar sólo para variables cuantitativas.
2. La media es independiente de las amplitudes de los intervalos.
3. La media es muy sensible a las puntuaciones extremas. Si tenemos una distribución con los siguientes pesos:
65 kg, 69kg , 65 kg, 72 kg, 66 kg, 75 kg, 70 kg, 110 kg.
La media es igual a 74 kg, que es una medida de centralización poco representativa de la distribución.
4. La media no se puede calcular si hay un intervalo con una amplitud indeterminada.
| xi | fi | |
|---|---|---|
| [60, 63) | 61.5 | 5 |
| [63, 66) | 64.5 | 18 |
| [66, 69) | 67.5 | 42 |
| [69, 72) | 70.5 | 27 |
| [72, ∞ ) | 8 | |
| 100 |
En este caso no es posible hallar la media porque no podemos calcular la marca de clase de último intervalo.
